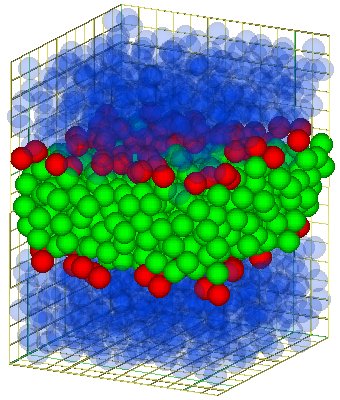
Bending elasticity of membranes of model surfactants

It has been discussed before that the bilayers made out of model surfactants are in fluid state. Therefore they don't show shear elasticity, but stretching elasticity [1,2]. Now for system which are are quasi infinite in two dimensions and thin in the third dimension, in other words for systems like membranes one has to take account another type of elasticity, namely the bending elasticity. This kind of elasticity is described by the Helfrich Hamiltonian. Unfortunately there is no way of bending a model bilayer in a controlled way without changing the boundary conditions. Hence one may think that its is impossible to check this Hamiltonion on this quasi molecule level.

However, one can't check it directly, but the Helfrich Hamiltonian predicts a spectrum of shape fluctuations of the membrane.

.

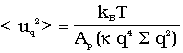Therefore I developed together with Dr. Gompper ( new location) a method to determine this spectrum for my model bilayers. But in contrast to the Helfrich theory we measure the the mean surface (for details, see [1,3]) rather than the neutral surface. In order to have a reasonable number of fluctuation modes the system size was extended to 576 (24x24) surfactants per monolayer and 11520 particles in total.

The spectrum we found this way for the almost tension-free bilayer can be fitted by

.

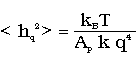However one should take two points into account if one compares those two formulas:

• First they might additional contribution to the spectrum arising from effects on molecular length scales. One candidate would protrusions as described in [4].
• Molecular excitations are be added to the neutral surface in the mean surface.

Therefore one should take the spectrum found to be the sum of a spectrum of the Helfrich type (1) (with =0) and a spectrum of molecular excitations. The protrusions mentioned before would lead to a spectrum which decays with

.

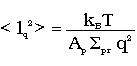Hence this spectrum can be interpreted as the bending spectrum and a protrusion spectrum.

For membranes with non-vanishing tension one has to included the -term in (1) into (2). Since the tension can be determined independently (see the page about the stretching elasticity), one has still only two fitting constants. It turns out that correction of tension is necessary to fit the spectra for non vanishing tension. Even in extreme case (i.e. strong lateral compression) this approach give reasonable values.

The bending rigidities found this way are about 7 kBT. This value is in the range typical for lipid-membranes. The cross over between the regime of the protrusion and the bending modes occurs about at an equivalent of 6-8 surfactants along the mode. At this point the wave length and the thickness of the bilayer became comparable.

Conclusion

It turns out that down to almost molecule dimension, the Helfrich Hamlitonian applies. If wave length and the thickness of the bilayer became comparable other molecular effects, namely protrusions became important. However even below this point the Helfrich Hamlitonian may apply.

Literature:

1. R. Goetz; PhD-thesis, Universität Potsdam 1997.
2. R. Goetz, R. Lipowsky; J. Chem. Phys. 108, (1998), 7397-7409
3. R. Goetz, R. Lipowsky; Phys. Rev. Letters 82, (1999), 221-224
4. R. Lipowsky, S. Grotehans; Biophys Chem 49 (1994); 27-34